齐夫定律(英语:Zipf’s law,IPA英语发音:/ˈzɪf/)是由哈佛大学的语言学家乔治·金斯利·齐夫(George Kingsley Zipf)于1949年发表的实验定律。它可以表述为:在自然语言的语料库里,一个单词出现的频率与它在频率表里的排名成反比。所以,频率最高的单词出现的频率大约是出现频率第二位的单词的2倍,而出现频率第二位的单词则是出现频率第四位的单词的2倍。这个定律被作为任何与幂定律概率分布有关的事物的参考。
最简单的齐夫定律的例子是“1/f function”。给出一组齐夫分布的频率,按照从最常见到非常见排列,第二常见的频率是最常见频率的出现次数的½,第三常见的频率是最常见的频率的1/3,第n常见的频率是最常见频率出现次数的1/n。然而,这并不精确,因为所有的项必须出现一个整数次数,一个单词不可能出现2.5次。
在Brown语料库中,“the”、“of”、“and”是出现频率最前的三个单词,其出现的频数分别为69971次、36411次、28852次,大约占整个语料库100万个单词中的7%、3.6%、2.9%,其比例约为6:3:2。大约占整个语料库的7%(100万单词中出现69971次)。满足齐夫定律中的描述。仅仅前135个字汇就占了Brown语料库的一半。
齐夫定律是一个实验定律,而非理论定律,可以在很多非语言学排名中被观察到,例如不同国家中城市的数量、公司的规模、收入排名等。但它的起因是一个争论的焦点。齐夫定律很容易用点阵图观察,坐标分别为排名和频率的自然对数(log)。比如,“the”用上述表述可以描述为x = log(1), y = log(69971)的点。如果所有的点接近一条直线,那么它就遵循齐夫定律。
 横纵坐标均为对数比例下,齐夫定律的概率质量函数的图像,其中N = 10。横坐标是指数k 。(注意,函数仅在k为整数时有定义,图上的连线不代表函数时连续的。) 概率质量函数
|
|
 横纵坐标均为对数比例下,齐夫定律的累计分布函数的图像,其中N = 10。横坐标是指数k 。(注意,函数仅在k为整数时有定义,图上的连线不代表函数时连续的。) 累积分布函数
|
|
| 参数 | 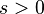 (实数) (实数)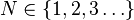 (正整数) (正整数) |
|---|---|
| 支撑集 | 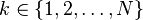 |
| 概率質量函數 | 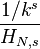 |
| 累积分布函数 | 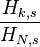 |
| 期望值 | 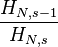 |
| 众数 |  |
| 信息熵 | 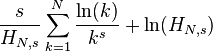 |
| 动差生成函数 |  |
| 特性函数 |  |
本文内容来自维基百科:
http://zh.wikipedia.org/wiki/%E9%BD%8A%E5%A4%AB%E5%AE%9A%E5%BE%8B